

|
액추에이터 플런저(plunger)의 거동해석은 플런저의 이동 방향과 자기 시스템에서 발생하는 자기력(magnetic force) 방향이
z축만으로 구속되었다는 가정에서 외력 Fm, 플런저의 질량 m1, 스프링 k1 으로 구성된 1자유도계 운동방정식으로 모델링이 가능하다.
또한 플런저의 동작이 일정거리의 구속조건을 가지고 있기 때문에 충돌시 유체점성에 의해 발생하는 감쇠(damping) c1,
금속 충돌을 모사하기 위한 금속의 등가강성(equivalent stiffness)과 등가감쇠(equivalent damping) k2,c2,k3,c3 등도
고려하여야 한다. 이를 고려한 플런저의 동적모델은 다음과 같다.
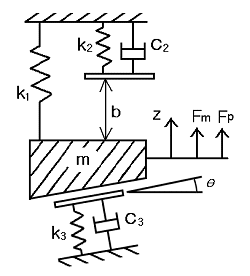
운동모델에서 z 를 플런저의 변위로 하고 Newton 법칙을 적용하여 운동방정식을 구하면 식(1)가 얻어진다.
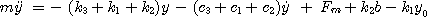 (식1)
(식1)
여기서, y0 는 코일스프링의 초기변위이고 b 는 초기상태의 공극(air gap)의 크기이다. 또한 k1
는 코일스프링 상수,
c1은 내부 유체유동에 의한 감쇠, k2 와 c2
는 플런저와 코어의 충돌시의 등가강성과 등가감쇠, k3
, c3는 플런저와
밸브시트(valve seat)면 충돌시의 등가강성과 등가감쇠이다.
운동방정식 식(1)에 상하의 구속조건을 표현하기 위해 식(2)의 분리조건을 부여하고 4차 Runge-Kutta 법을 적용하여
진동해석의 수치해를 구할 수 있다.
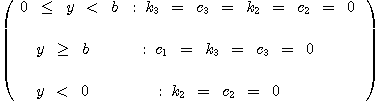 (식2)
(식2)
또한, 운동방정식의 수치해석을 통해 플런저의 이동이 발생하면 자기장 유한요소 해석에 사용되는 격자들의 형상이 바뀌게 된다.
이를 자기장 유한요소 해석에 반영하기 위해 일정거리 이상의 플런저 이동이 발생하면 플런저 격자들을 이동시켜 주어
다음 시간스텝의 유한요소해석에 적용되게 하고 있다.
| ⓒ 2003-2024 왕복전동 액추에이터·솔레노이드 연구회 All rights reserved. |