연자성체와 솔레노이드의 자기력
일반 서적에서 간단하게 솔레노이드의 자기력을 계산할때 공극부분의 자기저항만을 고려해 구하고 있습니다.
식을 유도해보면, 먼저 아래의 식으로 공극부의 자기저항을 구합니다.
Lg
Rmg = ----- (Lg : 공극부의 유효길이, Ag : 공극부의 단면적)
μ0 Ag
다음으로 공극부의 자기저항으로 자속밀도를 계산합니다.
N I
Bg = ------ ( N: 코일 턴수, I : 전류 )
Rmg Ag
마지막으로 자속밀도로 공극부에서 발생하는 자기력을 계산합니다.
Bg^2 Ag
Fm = -------- ( μ0 : 진공의 투자율 )
2 μ0
이런 유도과정에서 자기회로를 이루고있는 자성체는 언급이 되고있지 않기 때문에
자기회로를 이루고 있는 연자성체(core,case,plunger등)의 자기특성과 자기력은
상관이 없다고 생각할 수 있습니다.
유도과정의 가정으로 '누설자속이 없고, 철심의 자기저항을 무시한다'라고 합니다.
여기서, 누설자속은 일반적으로 무시할수 있습니다. 하지만 철심의 자기저항을
무시할수 있는 조건은 자성체의 자화가 BH 곡선의 선형구간에서만 가능한것입니다.
μ = B/H 에서 보듯이 투자율을 아래 BH 곡선의 기울기이고,
자성체의 투자율이 공기에 비해서 1000배 이상이라고 하는 것은 아래 그림의
파란선에 해당하는 최대 투자율을 크기입니다.
즉, 선형구간에서는 이 투자율이 공기 투자율에 비해 아주 크다고 할 수 있습니다.
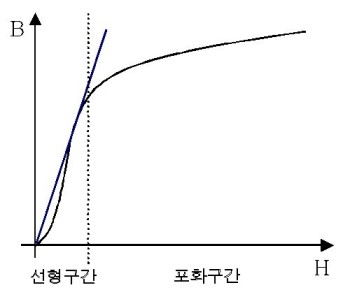
하지만 실제 솔레노이드의 작동에서 상대적으로 면적이 좁은 코어부분의 자화는
BH곡선의 선형구간을 지나서 자기 포화구간으로 접어들게 됩니다.
자성체의 자속이 포화가 되면 자성체의 투자율은 자계의 세기(H)값을 증가시켜도
자속밀도(B)가 거의 증가하지 않는 공기의 투자율과 비슷하게 됩니다.
결국, 자성체가 자기포화가 되면 철심의 자기저항을 무시한다는 가정이 힘들게되고,
위에서 언급한 식만으로는 계산이 불가능하게 됩니다.
따라서 연자성체의 비선형 자화특성을 고려한 유한요소해석이 필요합니다.
참고로 솔레노이드밸브의 자기력계산”글에서 자성체의 투자율 변화를
고려한 수계산 방법을 언급하였습니다. 참고하세요.
|
ⓒ 2003-2024 왕복전동 액추에이터·솔레노이드 연구회 All rights reserved.
|


