솔레노이드의 자기력

솔레노이드의 자기력

솔레노이드의 코일에 전류가 인가될 때
플런저에서 발생하는 자기력은 두 영구자석 사이에서 발생하는 힘과 같이
헤밀턴의 원리(물리계는 저장에너지가 최소인 방향으로 힘을 받음)에 의해 발생합니다.
즉, 플런저와 코어가 자화가 되어 두 영구자석처럼 서로 인력을 발생시키는 것입니다.

이때의 자기력을 가정을 통해 간단한 수식으로 나타내면 다음과 같습니다.

        Bg^2 * Ag
Fm = -----------   ( 여기서,   Bg : 자기력이 발생하는 공극부의 자속밀도,
        2 *  μ0                             Ag : 자기력이 발생하는 공극부의 단면적,
                                               μ0 : 진공의 투자율   )

여기에서 진공의 투자율 (μ0) 은 상수이고,
공극부의 면적(Ag) 또한 설계형상이 결정되면 일정한 값입니다.
따라서, 솔레노이드 자기력은 공극부의 자속밀도 Bg로 조절이 가능합니다.

B는 자속의 밀도이므로 자속을 면적으로 나눈 값 입니다.

       Ф
Bg = ---             ( 여기서, Ф : 자속량 )
       Ag

결국, 솔레노이드의 자기력은 자기회로에 흐르는 자속량을 구하면 계산이 가능합니다.

자속량을 간단하게 계산하기 위한 방법으로
자계를 전기회로와 유사한 자기회로로 가정하면,
솔레노이드의 자기력을 전기회로 계산법과 유사하게 계산할 수 있습니다.
먼저, 자기회로의 변수들을 이해하기 위해서 전기회로와 비교하면 다음과 같습니다.
( 솔레노이드 코일에 전류를 인가하면 코일을 중심으로 주위의 자성체(금속)과 공극을
지나는 자속이 발생합니다. 이 자속의 통로를 자기회로라고 합니다.)

전기회로        자기회로
I (전류)         Φ (자속)
V (전압)        NI (mmf : magnetomotive force, 기자력), N : 코일 회전수, I : 전류
R (저항)        Rm (자기저항 : reluctance)
여기서 기자력(MMF) 은 자계(磁界)를 일으키는 원천이 됩니다.

이처럼 가정을 하면, 전기 오옴의 법칙처럼 자기의 오옴의 법칙이 성립하고
다음과 같이 자속을 계산할 수 있습니다.

       N * I
Ф = ------          (여기서, N : 권선코일수, I : 코일의 전류 )
       Rm

여기서 Rm 은 기자력 NI 을 인가할때 발생하는 자속량 Ф 의 크기를 나타내는 전체 자기저항 입니다.

솔레노이드에서 발생하는 자속은 케이스, 코어, 플런저, 공극을 지나면서 폐루프를 형성하고 있습니다.
즉, 자기회로는 하나의 자기저항으로 이루어진 것이 아니라
아래의 그림처럼 투자율, 자속통과 길이, 자속통과 단면적이 다른 여러 개의 자기저항이
직 ·병렬로 연결된 것으로 표현합니다.

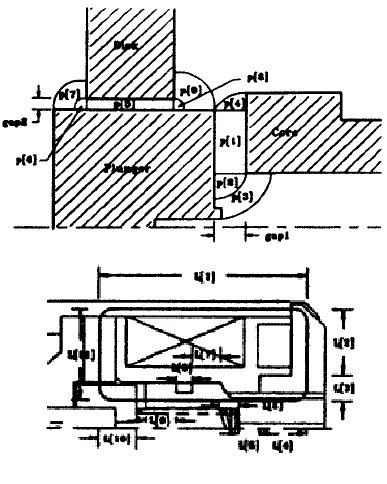
따라서 전체 자기저항 Rm 은 전기저항과 같이 자기회로 안의 자기저항의 합으로 표현이 가능합니다.
직렬로 연결된 경우는

Rm = Rm1 + Rm2 + … + Rmn 으로 계산하고,

병렬로 연결되는 경우는
                        1
Rm = -------------------------- 으로 계산이 됩니다.
            1/Rm1 + 1/Rm2 + … + 1/Rmn

위 식들의 분할된 영역의 자기저항은 다음의 식으로 계산 가능합니다.

        Li
Rmi = -----        (여기서, Li : 분할된 영역을 자속이 통과하는 길이,
       μi * Ai                μi : 자성체의 BH 곡선을 통해 계산되는 투자율, Ai : 분할된 영역의 단면적)

이제 분할된 영역의 자기저항을 구하면 거슬러 올라가면서
전제 자기저항을 구하고, 발생 자속량을 계산할 수 있고, 자속량으로 공극의 자속밀도를 계산하고,
플런저에 발생하는 솔레노이드의 자기력을 계산 할 수 있습니다.

지금까지 자기회로를 이용하여 솔레노이드에 발생하는 자기력 계산법을 간단히 훑어 보았습니다.
결국, 솔레노이드의 자기력은 공극에서 발생하는 자속밀도의 자승에 비례하는 값으로
코일의 회전수(N)과 코일 전류(I), 자성체의 투자율(μ )의 자승에 비례하고,
자속이 통과하는 길이의 자승에 반비례한다. 또한 자속이 통과하는 자기회로의 단면적에도 영향을 받고 있습니다.
계산과정을 보면 단순한 식의 조합으로 자기력이 계산 되는 것으로 보여지나,
자기회로를 이용한 계산에서도 어려운 문제는
자성체의 투자율이 일정한 값이 아니라 아래의 그림처럼 비선형 특성을 가지고 있다는 것입니다.

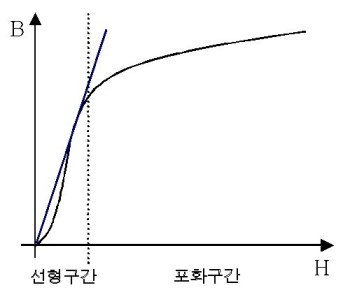
때문에 코일 회전수나 코일 전류를 증가시킬 때 자기력이 어느 정도까지만 증가하다가 더 이상 증가하지 않게 되는 것입니다.
따라서 실제 솔레노이드의 자기력을 계산할 때는 수치해석의 반복법을 적용하여 계산하여야 합니다.

또한 가정자로법의 사용한 계산은 자기저항 분할영역의 개수에 한계가 있기 때문에
전체적인 계산결과를 보기에는 효과적이지만 국소부분의 설계변경에서는 적용하기가 어렵습니다.
이런 경우에는 유한요소법(FEM) 기법을 사용한 전자기장 전산해석이 필요합니다.